What-now: graficando dependencias
No se resuelve con un par de líneas
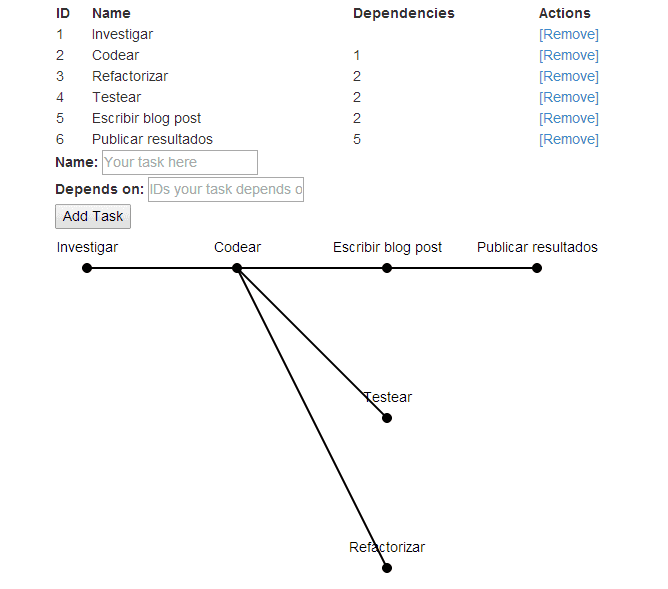
Desde hace un par de semanas estoy trabajando en lograr que el proyecto de what-now grafique dependencias entre tareas: si una tarea depende de otra, una línea debería conectarlos. Esta tarea básica fue muy simple, pero lo desafiante fue lograr que se graficaran de forma que las líneas se cruzaran entre ellas lo menos posible.
Aquí contaré sobre este logro y sobre lo que aprendí en el proceso.
Graficar dependencias en d3
Graficar las dependencias entre las tareas probó ser algo realmente simple. Se trata de simplemente agregar objetos line y asegurarnos de poner sus coordenadas y un stroke para que la línea se vea.
La investigación: minimizar cruces
Tras graficar las dependencias, me di cuenta que era muy simple que dos tareas tuvieran cruces o que la forma del grafo estuviera lejos de ser óptima. Ya sabía que quería organizar las tareas en “capas”, en donde cada capa sólo incluye tareas que dependen de las capas anteriores, de forma que las dependencias solo fluyan hacia atrás (o hacia adelante, dependiendo de cómo lo miren).
Este proceso es simple, pero la ubicación de los nodos es una misma capa no lo es tanto. Pensé un poco al respecto y no encontré ninguna respuesta obvia, por lo que pensé que era un buen momento para investigar sobre algoritmos de layout. Estos son algoritmos que me permitirían determinar la posición apropiada de los nodos para minimizar la cantidad de cruces y la forma general del grafo.
Distintas soluciones para distintos tipos de grafos
Claro, según cada caso particular, existen muchos algoritmos particulares para distintos tipos de grafos. Y tiene sentido: querremos ordenar los nodos de forma distinta según tengamos un grafo con bucles, un grafo acíclico, un árbol binario o tantas otras opciones. No existen algoritmos ni óptimos ni genéricos por la amplia variedad de posibles situaciones. Y más aún, los criterios de legibilidad para cada uno de estos varía ampliamente, con lo que para lo que un algoritmo hace bien, el otro arrojaría resultados desagradables a la vista.
Hay un algoritmo particular basado en “fuerzas” (Fruchterman–Reingold), que de hecho es muy ingenioso en su lógica. Si imaginamos que cada nodo repele a los otros nodos y simulamos esas fuerzas de repulsión, pero a la vez simulamos límites elásticos según los vértices que los unen, muchas veces el gráfico se “acomoda solo” tras una serie de iteraciones. Más interesante aún, esta es una característica ya incluída en d3: Force Layouts.
Intenté un par de aproximaciones pero me dí cuenta que esta solución no aplicaba a mi caso: yo necesitaba reordenar mis grafos sin romper la estructura de capas. Sin embargo, hay algoritmos propios para el dibujado de grafos en capas, y para quien esté interesado, hay un muy buen capítulo disponible online sobre Hierarchical Drawing Algorithms (PDF). Es un poco técnico y algo pesado en su lectura, porque cubre muchas posibilidades y comparaciones de algoritmos para cada uno de los pasos.
El algoritmo de Sugiyama
En mi búsqueda, encontré que uno de los algoritmos más utilizados y reconocidos como simples y eficientes es el algoritmo de Sugiyama. A continuación pueden ver un video de cómo se utiliza este algoritmo para producir un gráfico y minimizar sus cruces:
https://www.youtube.com/watch?v=n3tG0AKwiRE
El autor de este video (Lejf Diecks) tiene una serie de posts en donde explica el algoritmo. Ellos se pueden ver aquí:
- Sugiyama algorithm – Part 1
- Sugiyama algorithm – Part 2
- Sugiyama algorithm – Part 3
- Sugiyama algorithm – Part 4
La explicación básicamente expone los siguientes pasos:
- Separar a los nodos en capas según los vértices que lleguen a ellos
- Insertar nodos ficticios en vértices que alcancen más de dos capas
- Minimizar los cruces enfocándose entre las capas n y la n+1
- Remover los nodos ficticios
El punto 3. es particularmente especial, y merece una explicación propia: el objetivo de insertar los nodos ficticios (punto 2.) es sólo para simplificar este paso, que es un problema NP-difícil de por sí. El punto 4. también debe ser agregado por consecuencia del punto 2., ya que no queremos graficar estos nodos ficticios, sino que los usamos como herramienta de simplificación.
Tras agregar los nodos ficticios, podemos concentrarnos entre los cruces de las capas n y n+1, sin pensar en vértices que vayan en más de una capa. Esto significa que nuestras comparaciones para detectar cruces pueden basarse sólamente en la posición relativa de los nodos dentro de las capas, y no hay necesidad de hacer cálculos trigonométricos (que también podrían ser afectados por detalles de posicionamiento de nuestro grafo: separación de los nodos, ancho de los vértices, etc).
1. Separar a los nodos en capas
La separación de los nodos en capas es un problema simple de resolver, pero sólo si estamos asumiendo ciertas condiciones como las estoy asumiendo yo. Particularmente, estoy asumiendo que se trata de un grafo acíclico, es decir, en donde no habrá ciclos formados. En mi caso, si la tarea A depende de la tarea B, no tiene sentido que la tarea B dependa de la tarea A. De no tener esta restricción, es necesario convertir al grafo en uno acíclico.
La forma de entonces clasificar a los nodos en capas es:
- Inicializar un listado de nodos con todos los nodos del grafo:
nodesToVisit ← graphNodes - Inicializar un listado de nodos incluidos en el grafo, vacío:
visitedNodes ← [] - Inicializar el listado de capas que devolveremos vacío:
layers ← [] - Inicializar el listado de nodos que conforma la primera capa, vacío:
currentLayer ← [] - Iteramos por cada nodo a visitar:
for each currentNode in nodesToVisit- Si cada dependencia del nodo está entre los nodos ya visitados:
if containsAll(visitedNodes, currentNode.previousNodes)- Agregar el nodo a la capa actual:
currentLayer.add(currentNode) - Eliminar el nodo visitado del listado de pendientes:
nodesToVisit.remove(currentNode)
- Agregar el nodo a la capa actual:
- Si cada dependencia del nodo está entre los nodos ya visitados:
- Agregar la capa generada al listado de capas a devolver:
layers.add(currentLayer) - Si todavía quedan nodos pendientes a visitar:
if nodesToVisit.length > 0- Agregar todos los nodos de la capa actual a los nodos disponibles como dependencias:
visitedNodes.addAll(currentLayer) - Iterar desde el paso 4. inclusive.
- Agregar todos los nodos de la capa actual a los nodos disponibles como dependencias:
- Devolver el listado de capas generado:
return layers
Asumo que debe haber formas mucho más eficientes de generar este listado, pero creo que esta es lo suficientemente simple como para ser fácilmente comprensible. Esta solución es del orden de O(n2m) (n: cantidad de nodos, m: cantidad de dependencias de un nodo) lo cual hace que no se comporte nada bien para grandes cantidades de nodos.
2. Insertar nodos ficticios en vértices que alcancen más de dos capas
Como ya lo mencioné antes, el objetivo de este paso es poder simplificar los cálculos más adelante, lo cual significa que no es enteramente necesario, pero para evitar otras explicaciones más específicas, elegiré utilizar este método.
Cuando se generaron las capas, es posible haya nodos en la capa n que no tengan ningún nodo siguiente en la capa n+1. Esto es porque los nodos siguientes pueden a su vez tener dependencias en la capa n+1, lo que los habría colocado en la capa n+2. Por ejemplo: A1 y A2 no dependen de ningún nodo, con lo que se posicionan en la capa 1. B depende de A1, con lo que se posiciona en la capa 2. C depende de A2 y de B. Por su dependencia con B, C será posicionado en la capa 3, pero los nodos siguientes de A2 no se encuentran en la capa siguiente a la suya.
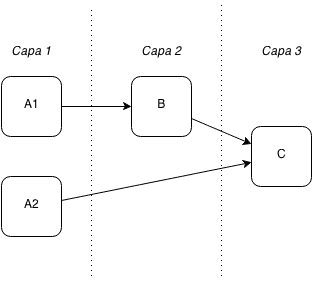
En un caso así, insertar un nodo ficticio en la capa 2 nos permitirá poder evaluar cruces entre esa capa y la anterior sin necesidad de evaluar ángulos de inclinación, o sin tener en cuenta nodos siguientes que puedan estar en capas totalmente separadas, haciendo nuestras comparaciones mucho más simples.
El proceso es tan simple como se puede ver a continuación:
- Iteramos por cada columna:
for each currentColumn in grid- Identificamos la columna siguiente:
nextColumn - Iteramos por cada nodo en la columna:
for each currentNode in currentColumn- Iteramos por cada nodo siguiente:
for each nextNode in currentNode.nextNodes- Si el nodo siguiente no está en la columna siguiente:
if (!nextColumn.contains(nextNode))- Crear un nodo falso que podamos identificar:
fakeNode - Desconectar el nodo actual de su siguiente:
disconnectNodes(currentNode, nextNode) - Conectar el nodo actual con el nodo falso:
connectNodes(currentNode, fakeNode) - Conectar el nodo falso con el nodo siguiente:
connectNodes(fakeNode, nextNode) - Insertar el nodo falso en la columna siguiente:
nextColumn.add(fakeNode)
- Crear un nodo falso que podamos identificar:
- Si el nodo siguiente no está en la columna siguiente:
- Iteramos por cada nodo siguiente:
- Identificamos la columna siguiente:
3. Minimizar cruces
Aún con los cambios que hemos logrado hasta este punto, la minimización de los cruces sigue siendo un problema difícil. La razón es que es fácil acomodar un par de nodos para evitar cruces y a la vez generar otros cruces en otras columnas. Finalmente, es posible que no exista una configuración que nos libre de cruces, si es que nuestro grafo está poblado de muchas dependencias. En casos como estos es cuando el algoritmo se comportará de la peor forma, o requerirá de una aproximación más avanzada para ser resuelto apropiadamente.
Lejf Diecks contaba en sus artículos originales que esto podía resolverse con un algortimo de búsqueda, posiblemente una búsqueda con ajustes para evitar mínimos locales que nos impidan acercarnos al mínimo global de cruces.
La forma de calcular cruces a este punto es bastante simple: ya que la representación de los nodos en columnas tienen sus índices alineados con la posición del nodo en la columna y como cada nodo sólo tiene nodos siguientes en la columna siguiente, sólo tenemos que comparar los índices. él habla de cuatro situaciones en las cuales sólo dos serán cruces, pero dado que debemos seguir un orden de evaluación, aproveché eso para reducir todo a una única condición.
A la vez, aproveché el orden de evaluación para mantener los cambios sobre la parte del grafo que aún no ha sido evaluada por cruces. Esto significa que podríamos mejorar la cantidad de cruces que tendremos hasta ahora, y llegando al final sólo tendremos que hacer lo mismo asegurándonos de no afectar lo que ya ordenamos antes.
El algoritmo se vería algo así:
- Iteramos por cada columna:
for each column in grids- Identificamos la columna siguiente:
nextColumn - Iteramos por cada nodo en la columna:
for each node1 in column- Iteramos por cada nodo que está debajo de este nodo en la columna:
for each node2 in column[node2..last]- Iteramos por cada nodo siguiente del primer nodo:
for each nextNode1 in node1.nextNodes- Iteramos por cada nodo siguiente del segundo nodo:
for each nextNode2 in node2.nextNodes- Identificamos la posición del siguiente del primer nodo:
nextNode1Index ← nextColumn.indexOf(nextNode1) - Identificamos la posición del siguiente del segundo nodo:
nextNode2Index ← nextColumn.indexOf(nextNode2) - Si el siguiente del segundo nodo tiene un índice menor al siguiente del primer nodo, tenemos un cruce:
if (nextNode2Index < nextNode1Index)- Intercambiamos los lugares de los nodos siguientes que producen el cruce:
swap(nextColumn, nextNode1, nextNode2)
- Intercambiamos los lugares de los nodos siguientes que producen el cruce:
- Identificamos la posición del siguiente del primer nodo:
- Iteramos por cada nodo siguiente del segundo nodo:
- Iteramos por cada nodo siguiente del primer nodo:
- Iteramos por cada nodo que está debajo de este nodo en la columna:
- Identificamos la columna siguiente:
El resultado no es ciertamente óptimo, pero considero que es lo suficientemente bueno como para la demostración. En el artículo original de Lejf Diecks, él recomendaba la generación de un algortimo genético, que permitiría alcanzar un máximo tras unas cuentas iteraciones, haciendo el proceso muy rápido. La idea me parece interesante, pero he elegido no implentarla todavía. Sin embargo, sé que sería fácil crear la función de evaluación, ya que solamente se trataría de contar la cantidad de cruces y el objetivo sería minimizarlos (0 sería un caso definitivamente óptimo que podría terminar la generación de forma temprana). Para mayor estética visual, podría agregarse el criterio de la cantidad de vértices inclinados, en donde también menos es mejor. Por otro lado, también es fácil la generación de cada una de las entidades, ya que sólo hay que modelar la posición de cada uno de los nodos, sin necesidad de variar las capas en la que cada nodo se encuentra. Finalmente, incluso se podría permitir que el algoritmo genético utilice más filas que la cantidad de nodos que existen en una fila (creando así la posibilidad de abrir paso a colocar nodos más alejados para que otros cruces no se produzcan).
Así es que se vería el código resultante:
4. Remover nodos falsos
En este punto, ya no hacen falta los nodos falsos que habíamos creado, de forma que podemos eliminarlos. Esto es tan simple como recorrer todo el grafo y quitar los nodos falsos, conectando nuevamente los nodos que estén detrás y adelante del nodo falso.
Podríamos simplemente asumir que los nodos falsos tienen un único predecesor y que tienen un sólo siguiente, por la forma en la que los hemos colocado anteriormente, pero en este caso asumiré que no es el caso. Esto es porque una futura posibilidad de estos nodos falsos es que sean conectados a varios nodos y que reemplacen otros posibles cruces – pero eso es historia para otro día. Sea como sea, también es buena idea que asumamos casos más genéricos, lo que nos permitirá más adelante refactorizar este código en algo más reutilizable.
Nuestro algoritmo para esto sería:
- Iteramos por cada columna:
for each column in grid- Identificamos el nodo actual:
node - Si es un nodo falso:
if (isFakeNode(node))- Iteramos por cada nodo previo:
for each previousNode in node.previousNodes- Iteramos por cada nodo siguiente:
for each nextNode in node.nextNodes- Conectamos el nodo previo con el nodo siguiente:
connectNodes(previousNode, nextNode)
- Conectamos el nodo previo con el nodo siguiente:
- Desconectamos el nodo previo del nodo falso:
disconnectNodes(previousNode, node)
- Iteramos por cada nodo siguiente:
- Iteramos por cada nodo siguiente:
for each nextNode in node.nextNodes
- Iteramos por cada nodo previo:
- Desconectamos el nodo siguiente del nodo falso:
disconnectNodes(node, nextNode) - Eliminamos el nodo falso de la columna:
column.remove(node)
- Identificamos el nodo actual:
Y en código se puede ver así:
Otros pensamientos
El unit testing me generó alarmas sobre el diseño
El unit testing me resultó difícil y antinatural en este caso. En mi mente, tener un servicio que implementara el algoritmo de Sugiyama era una única responsabilidad y por tanto una buena idea para estar aislado en uno y sólo un servicio. Sin embargo, me di cuenta que es muy difícil poder probarlo de comienzo a final sin tener en cuenta todos los pasos intermedios, y como yo no quería que mi servicio expusiera su comportamiento interno, era imposible para mi partirlo en unidades más pequeñas para unit testear.
Esto me hace pensar que mi servicio no es tan unitario como yo lo pensaba – si es difícil de testear como unidad, quizá no es una unidad después de todo. Mi solución temporal ha sido exponer algunos métodos internos de este servicio y testearlos, pero claramente podría todo convertirse en un módulo y tener una clase de facade que exponga los que yo necesito utilizar en mi aplicación mientras el resto es unit testeado como unidades independientes.
La complejidad ciclomática me generó alarmas sobre la performance
Por otro lado, encontré que existen muchas variantes de implementación y quizá considere alterar la que estoy usando a una más. Más allá del experimento, es posible que se vuelva muy ineficiente esta aplicación si es que estamos hablando de una cantidad grande de nodos. Miren la cantidad de bucles anidados que tienen los algoritmos que describí antes – no hay forma que eso sea eficiente en números grandes.
No sólo eso hace que sea ineficiente, también es difícil de seguir y me forzó a partirlo en unidades más pequeñas sólo para poder probar. Si no puedo seguir el método mentalmente, está claro que debería partirlo en partes más pequeñas.
Explicar cómo lo hago me hizo replantearme decisiones
Muy curiosamente, no noté mucho de esto hasta el momento en que escribí este artículo y al momento de explicarlo me di cuenta que las soluciones eran exageradamente complicadas o innecesariamente ineficientes. Probablemente no lo vean, pero hubo varios cambios que hice sólo al momento de explicar esto porque la versión anterior era peor aún.
Quizá tenga que comprarme un patito de goma.
La pasión por el producto mismo
Cuando comencé este proyecto, tenía en mente sólo hacer lo más básico posible como una excusa para experimentar con d3js. Sin embargo, ahora que lo veo semi-funcional me daría lástima no terminar de generar un producto – posiblemente siga agregándole funcionalidad hasta que otras prioridades tomen lugar o hasta que llegue a un punto en donde realmente me sienta cómodo con él como producto final.
Conclusión
En este punto what-now tiene estas nuevas funcionalidades presentes en su versión online: http://what-now.heroku.com. La investigación de cómo lograr esto fue muy interesante y me llevó a encontrar varios conceptos que desconocía totalmente. Aún así, no quiero ahondar en ellos aún, sino que quiero continuar con este proyecto para que sea usable y para luego continuar con otros.
